Download the digital guide as a PDF file (216KB)

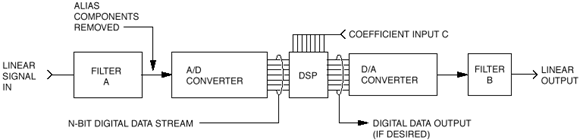
Digital (FIR and IIR) Electronic Filter Design Guide Digital-Signal-Processing Filters (DSP) Based on combining ever increasing computer processing speed with higher sample rate processors, Digital Signal Processors (DSP’s) continue to receive a great deal of attention in technical literature and new product design. The following section on digital filter design reflects the importance of understanding and utilizing this technology to provide precision stand alone digital or integrated analog/digital product solutions. By utilizing DSP’s capable of sequencing and reproducing hundreds to thousands of discrete elements, design models can simulate large hardware structures at relatively low cost. DSP techniques can perform functions such as Fast-Fourier Transforms (FFT), delay equalization, programmable gain, modulation, encoding/decoding, and filtering. Programs can be written where: Filter weighting functions (coefficients) can be calculated on the fly, reducing memory requirements or Algorithms can be dynamically modified as a function of signal input. DSP represents a subset of signal-processing activities that utilize A/D converters to turn analog signals into streams of digital data. A stand-alone digital filter requires an A/D converter (with associated anti-alias filter), a DSP chip and a PROM or software driver. An extensive sequence of multiplication’s and additions can then be performed on the digital data. In some applications, the designer may also want to place a D/A converter, accompanied by a reconstruction filter, on the output of the DSP to create an analog equivalent signal. Figure 1 shows a typical digital filter configuration.

		Digital Filters Digital filters process digitized or sampled signals. A digital filter computes a quantized time-domain representation of the convolution of the sampled input time function and a representation of the weighting function of the filter. They are realized by an extended sequence of multiplications and additions carried out at a uniformly spaced sample interval. Simply said, the digitized input signal is mathematically influenced by the DSP program. These signals are passed through structures that shift the clocked data into summers (adders), delay blocks and multipliers. These structures change the mathematical values in a predetermined way; the resulting data represents the filtered or transformed signal. It is important to note that distortion and noise can be introduced into digital filters simply by the conversion of analog signals into digital data, also by the digital filtering process itself and lastly by conversion of processed data back into analog. When fixed-point processing is used, additional noise and distortion may be added during the filtering process because the filter consists of large numbers of multiplications and additions, which produce errors, creating truncation noise. Increasing the bit resolution beyond 16-bits will reduce this filter noise. For most applications, as long as the A/D and D/A converters have high enough bit resolution, distortions introduced by the conversions are less of a problem1. 1. Theoretically, note that the ratio of the RMS value of a full-scale sine wave, to the RMS value of the quantization noise (expressed in dB) is SNR=6.02N + 1.76dB, where N is the number of bits in the ideal A/D converter. Although DSP's rarely serve exclusively as anti-alias filters (in fact, they require anti-alias filters), they can offer features that have no practical counterpart in the analog world. Some examples are 1) a linear phase filter that provides steep roll-off (near brick wall) characteristics or 2) a programmable digital filter that allows the signal conditioning to be changed on the fly via software, (frequency response or filter shape can be altered by loading stored or calculated coefficients into a DSP program). Instead of using a commercial DSP with software algorithms, a digital hardware filter can also be constructed from logic elements such as registers and gates, or an integrated hardware block such as an FPGA (Field Programmable Gate Array). Digital hardware filters are desirable for high bandwidth applications; the trade-offs are limited design flexibility and higher cost. Two Types of DSP's, Two Types of Math (1) Fixed-Point DSP and FIR (Finite Impulse Response) Implementations Fixed-Point DSP processors account for a majority of the DSP applications because of their smaller size and lower cost. The Fixed-Point math requires programmers to pay significant attention to the number of coefficients utilized in each algorithm when multiplying and accumulating digital data to prevent distortion caused by register overflow and a decrease of the signal-to-noise ratio caused by truncation noise. The structure of these algorithms uses a repetitive delay-and-add format that can be represented as "DIRECT FORM-I STRUCTURE", Figure 2.

FIR (Finite Impulse Response) filters are implemented using a finite number "n" delay taps on a delay line and "n" computation coefficients to compute the algorithm (filter) function. The above structure is non-recursive, a repetitive delay-and-add format, and is most often used to produce FIR filters. This structure depends upon each sample of new and present value data. FIR filters can create transfer functions that have no equivalent in linear circuit technology. They can offer shape factor accuracy and stability equivalent to very high-order linear active filters that cannot be achieved in the analog domain. Unlike IIR (Infinite Impulse Response) filters (See Item 2 below), FIR filters are formed with only the equivalent of zeros in the linear domain. This means that the taps depress or push down the amplitude of the transfer function. The amount of depression for each tap depends upon the value of the multiplier coefficient. Hence, the total number of taps determines the "steepness'" of the slope. This can be inferred from the structure shown in Figure 2 above. The number of taps (delays) and values of the computation coefficients (h0, h1,..hn..) are selected to "weight" the data being shifted down the delay line to create the desired amplitude response of the filter. In this configuration there are no feedback paths to cause instability. The calculation coefficients are not constrained to particular values and can be used to implement filter functions that do not have a linear system equivalent. Note: more taps increase the steepness of the filter roll-off while increasing calculation time (delay) and for high order filters, limiting bandwidth. The filter delay is easily calculated for the above structure. Delay = (0.5 x Taps)/Sampling rate. For example, a 300-tap filter with a sampling rate of 48 kHz yields a minimum 3.125 milli-second delay [(0.5 x 300)/48 = 3.125 milli-seconds]. Designers must also be aware of the tradeoffs between phase delay and filter precision when designing FIR filters. The bad news is that high order FIR filters have longer delay; the good news is that the phase response remains linear as a function of frequency. In applications where linear phase is critical and long phase delay cannot be tolerated, a linear active Bessel or a constant delay filter may be a better selection. Two very different design techniques are commonly used to develop digital FIR filters:

The Window Technique and The Equiripple Technique. A. Window's: The simplest technique is known as "Windowed" filters. This technique is based on designing a filter using well-known frequency domain transition functions called "windows". The use of windows often involves a choice of the lesser of two evils. Some windows, such as the Rectangular, yield fast roll-off in the frequency domain, but have limited attenuation in the stop-band along with poor group delay characteristics. Other windows like the Blackman, have better stop-band attenuation and group delay, but have a wide transition-band (the band-width between the corner frequency and the frequency attenuation floor). Windowed filters are easy to use, are scalable (give the same results no matter what the corner frequency is) and can be computed on-the-fly by the DSP. This latter point means that a tunable filter can be designed with the only limitation on corner frequency resolution being the number of bits in the tuning word. B. Equiripple: An Equiripple or Remez Exchange (Parks-McClellan) design technique provides an alternative to windowing by allowing the designer to achieve the desired frequency response with the fewest number of coefficients. This is achieved by an iterative process of comparing a selected coefficient set to the actual frequency response specified until the solution is obtained that requires the fewest number of coefficients. Though the efficiency of this technique is obviously very desirable, there are some concerns. For equiripple algorithms some values may converge to a false result or not converge at all. Therefore, all coefficient sets must be pre-tested off-line for every corner frequency value. Application specific solutions (programs) that require signal tracking or dynamically changing performance parameters are typically better suited for windowing since convergence is not a concern with windowing. Equiripple designs are based on optimization theory and require an enormous amount of computation effort. With the availability of today's desktop computers, the computational intensity requirement is not a problem, but combined with the possibility of convergence failure; equiripple filters typically cannot be designed on-the-fly within the DSP. 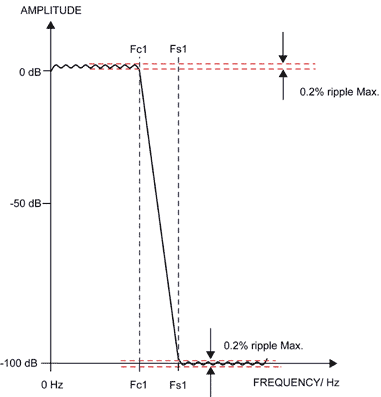Many people will use windowing such as a "Kaiser" window to produce good scalable FIR filters fairly quickly without the worry of non-convergence. However, if one is interested in producing the highest performance digital filter for a given hardware configuration, the iterative Remez Exchange algorithm is worth the test. Figure 3 illustrates a major advantage that a digital low-pass equiripple FIR filter can offer designers when solving signal-conditioning problems. FC1 and FS1 are the corner and stop-band frequencies respectively. The typical number of filter taps used for this -100 dB attenuation example is around 300. The ratio of FS1 to FC1 is 1.1, an unheard-of shape factor in the analog world. A slope calculation yields the fact that an analog filter would have to be a 30th order filter to achieve this performance! Analog filters beyond 10 poles are very difficult to realize and tend to be noisy.

(2) The Floating-Point DSP and IIR (Infinite Impulse Response) Implementations Like its name, Floating Point DSP's can perform floating-point math, which greatly decreases truncation noise problems and allows more complicated filter structures such as the inclusion of both poles and zeros. This permits the approximation of many waveforms or transfer functions that can be expressed as an infinite recursive series. These implementations are referred to as Infinite Impulse Response (IIR) filters. The functions are infinite recursive because they use previously calculated values in future calculations akin to feedback in hardware systems. The equivalent of classical linear-system transfer functions can be implemented by using IIR implementation techniques. A common procedure is to start with the classic analog filter transfer function, such as a Butterworth, and apply the required transform to convert the filter equations from the complex S-domain to the complex Z-domain. The resulting coefficients yield a Z-domain transfer function in a feedback configuration with a number "n" of delay nodes that is equal to the order of the S-domain transfer function. These implementations are referred to as IIR filters because when a short impulse is put through the filter, the output value does not converge quickly to zero, but theoretically continues decreasing over an infinite number of samples. Floating Point DSPs can produce near equivalent analog filter transforms such as Butterworth, Chebycheff and elliptic because they use essentially the same mathematical structure as their analog counterparts. For the same reason, they exhibit the same or worse non-linear phase characteristics as their analog counterparts since the equivalent of poles and zeros in linear systems are reproduced with an IIR, digital filter. Figure 4 illustrates a bi-quad digital filter structure that computes the response of a second order IIR transfer function. It has two delay nodes and the computation coefficients are A1k, A2k, B1k and B2k.

Floating Point processors do have some advantages over Fixed Point processors. Specific DSP applications such as IIR filters are easier to implement with floating point processors. Floating Point application code can have lower development costs and shorter time to market with respect to corresponding programs in a Fixed-Point format. Floating Point representation of data has a smaller amount of probable error and noise. After all is said, these powerful Floating-Point devices can emulate Fixed-Point processors but at higher hardware cost. Summary Complex digital filter functions involve millions of mathematical operations. The speed of these operations depends on a variety of factors; DSP chip speed, filter complexity (number of taps), and the number of bits of accuracy in each computation. Today, many DSP turnkey and application specific platforms are available along with development systems for the savvy engineer, who wishes to do his or her own design. Many computer programs also exist that can determine the number of taps and the values of computation coefficients that are required to implement a specific digital filter performance function. In some cases these programs output files directly to a PROM burner or Flash Memory, automatically loading programs (algorithms) into the actual DSP circuit. One such Software Program is MatLabTM by (The MathWorksTM) which calculates coefficients for designated FIR filters and can also produce IIR filter programs. Because of the many hardware and software design options and trade-offs available in providing signal processing solutions, having the availability of analog and DSP design and programming expertise along with application specific Intellectual Property (IP) from one source can provide a strong argument to the busy design engineer to seek a turnkey or custom solution from a manufacturer like Frequency Devices. Examples include: Multi-Rate FIR filters, which can significantly extend low frequency bandwidth limits and shorten filter delay; both are design limitations of single rate sampled DSP filter algorithms. Ultra low noise and distortion anti-alias and reconstruction filters to 120 dB. Low distortion signal generators to 20-bits. AD and DA signal converters with -100 dB or better noise floors. As DSP sample rates continue to increase, the bandwidth and performance of DSP solutions will also increase.

Signal Reconstruction Electronic Filter Design Guide Digital to Analog Conversion (D/A) As with input signals to A/D converters, waveforms created by D/A converters also exhibit errors. For each input digital data point, the D/A holds the corresponding value until the next sample period. Therefore, the output waveform exists as a sequence of steps. This output, a kind of "sample-and-hold" is known as a "first-order hold". Any step-function approximation of a smooth analog wave such as D/A output consists of a set of primary-frequency sinusoidals and their harmonics. To accurately recover the analog signal requires removing these harmonics, usually with a filter following the D/A. Such a filter features a very flat amplitude response in the pass-band and a rapid roll-off above fc. The stop-band floor must be deep enough to attenuate high-frequency component errors to below an LSB of the target system's A/D or D/A converter. Roll-off need not be as sharp as an anti-alias prefilter, which must push the target system's useful bandwidth as close as possible to the Nyquist frequency. Even if the original signal bandwidth is 100% of Nyquist (an unrealizable goal without serious alias errors), the lowest undesirable frequency in the D/A output is the second harmonic. For reasons of convenience, many designers specify the same filter for both anti-alias and reconstruction. From an attenuation standpoint, however, this approach represents overkill. In addition, because the step-function D/A output includes fast rise and fall times, a softer roll-off, more linear phase filter (Bessel) would work better at this end of the process because it produces less ringing and overshoot than an elliptic or similar sharp-roll-off transfer function does. According to Fourier-transform mathematics, a waveform reconstructed using a first-order hold exhibits an amplitude error (E) that varies as a function of frequency f and the sampling frequency fs, and whose magnitude is given by Figure 5. E = (Sin X) X , where X = f fs

Choosing a Filter Solution Electronic Filter Design Guide Choosing a filter technology is less straightforward than selecting a transfer function from among Butterworth, Bessel, and Cauer-elliptic. The best solution depends heavily on the application. To reduce alias errors to acceptable levels, designers base their filter implementation selections on the desired bandwidth and accuracy of the target system. These parameters, along with hardware costs, determine the system's speed (sampling rate), resolution (number of bits), type of A/D converter (sigma-delta, successive-approximation, flash, etc.), and anti-alias/reconstruction filter technology. Linear-Active Filters serve applications that require system bandwidths as close as possible to the sampling frequency, with a sharp cutoff. Simple two or three-pole versions also serve as anti-alias filters and clock feed-through or reconstruction filters for systems employing switched-capacitor or DSP solutions. With active filter technology, very accurate, low frequency filters in the 2.0 MHz to sub hertz range can be built that are almost impossible to achieve with other technologies. Switched-Capacitor designs work best where cost and space are at a premium. Other criteria to consider include: when required system accuracy is around 10 to 13 bits, the bandwidth is more than 10 kHz, and where the DC accuracy and stability specifications of switch capacitor filters are acceptable. Applications in the multi-megahertz range or requiring power line conditioning (filtering) typically utilize Passive Filters. This includes snubbers for high-energy inductive or transient suppression. Also, passive filters must be used when power is not available, though the user must be willing to tolerate insertion loss (signal attenuation). Digital Filters are used primarily when transfer-function requirements have no counterpart in the analog world, or when a DSP already resides on the circuit board to perform other functions. An example of a digital filter selection limitation is shown in Figure 6. The pass-band for a high-pass digital filter is limited to the maximum bandwidth, sampling rate, and word length that the filter order allows. After that, there is no pass-band! For this example, broadband high frequency active or passive filters are an obvious alternative.

Figure 6

Digital filter selection is the choice or trade-off between Floating Point DSP - IIR filters and Fixed Point DSP - FIR filters which are illustrated in the Digital Filter Decision Tree, Figure 7.

Whether you decide on a fixed point FIR or floating point IIR solution, the world is still analog. In many applications the conversion from analog to digital and back to analog is a requirement, often with limitations in bandwidth and design flexibility. One example is range limitation which is the maximum bandwidth imposed by the sampling when altering the digital filter frequency. A solution is to adjust the clock, which forces adjustments in the anti-alias and reconstruction filter, therefore requiring multiple fixed frequency or programmable filters (typically not cost effective). Another approach is to adjust the clock within the DSP by decimation or interpolation; hence the filter shape can be modified within the filter algorithm. This is called Multi-Rate filtering and several decimations can be implemented in series to reach very low frequencies. This Intellectual Property has been well refined by Frequency Devices engineers. SHOULD YOU BUILD IT YOURSELF? Electronic designers often try to ensure a product's signal integrity by constructing their own signal processing circuitry. Unfortunately, the time and money associated with engineering design and assembly efforts can make the actual cost of such a solution very high. The design may require a complex arrangement of sensitive components that consume precious board real estate and compromise system reliability. In addition, some of these components can generate their own alias signals. Design engineers generally understand their own applications very well. Typically, however, they are not signal-conditioning or signal-processing experts. Limited experience with integrated analog and DSP technology often make creating an effective and accurate filter solution difficult and time-consuming. On the other hand, system manufacturers are generally very sensitive to the cost of purchased solutions. The experts at Frequency Devices have seen many instances where companies have regarded self-contained signal conditioning modules and subassemblies as too expensive. Therefore, engineers design or buy simple, inexpensive alternatives for their products, hoping that lower cost and typically lower performing products will be good enough. Such approaches may work, but in many cases the reduced signal integrity degrades system performance to the point of unacceptability. Unfortunately, once in-house designs do not meet desired performance specifications, altering the design to incorporate the proper alternative solution or accepting the degraded signals, usually under extreme time pressures, generally costs far more than relying on better solutions in the first place would have. Reinventing the wheel rarely produces the most effective results. LET US HELP Based on many years of experience with special-purpose signal-conditioning devices and systems, Frequency Devices offers some of the most advanced signal-processing products in the industry. We will work with you to develop specifications that are appropriate to your unique needs, avoiding either under-specifying or over-specifying in the interest of controlling cost while maximizing performance. Whether prototyping to prove a design, looking for laboratory test equipment or working with high-volume applications for electronic original equipment manufacturers and process control, you can rely on Frequency Devices' data-acquisition, processing, and manipulation solutions for the test and measurement, aerospace, undersea, navigation, automatic test equipment, R & D, telecommunications, acoustic, and vibration markets. Frequency Devices offers a combination of turnkey, standard and custom module and subassembly solutions utilizing both analog and digital signal processing; providing engineers with choices and solutions consistent with their system or project requirements.